In the
first note (Ranking Before Prediction), I argued that many quantitative equity systems are not prediction engines but ranking systems. They normalize information, combine factors, induce an ordering, and act almost exclusively on the extremes of that ordering.
This naturally leads to the next question:
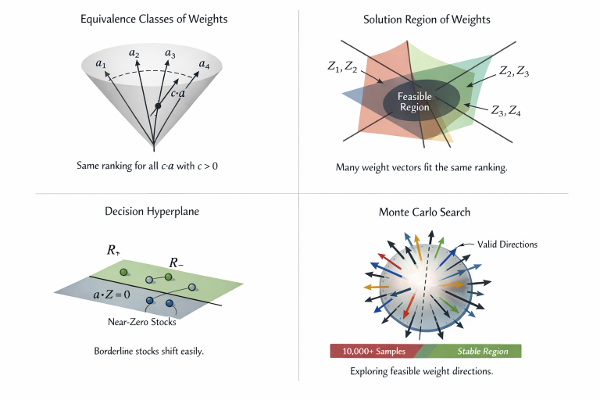
If ranking is the object, why not learn the factor weights that produce the correct ranking?
At first glance, this seems straightforward.
Given factor information at time
t and realized returns over a future window, why not infer the weights that would have generated the observed ordering?
This note explains why that question — weight recovery from realized rankings — is not well-behaved in the usual sense, why this difficulty is structural rather than technical, and why practitioners repeatedly converge on heuristics, constraints, Monte Carlo exploration, and stability analysis instead of precise coefficient estimation.
Please read the note in pdf